'520'又是一年表白日，三个个方法告白你最爱的’气球‘
本文共 5820 字，大约阅读时间需要 19 分钟。
不敢表白？
作为一个技术性宅男什么大风大浪没见过，然而面对喜欢的人却始终无法迈出那一步。最后眼睁睁地看着你心爱的人飞走这是很憋屈，很悲催的。不过没关系程序可以帮你表达你的想法！！！！！看不懂没关系，我们现在只要效果。
cmd命令表白
效果如下
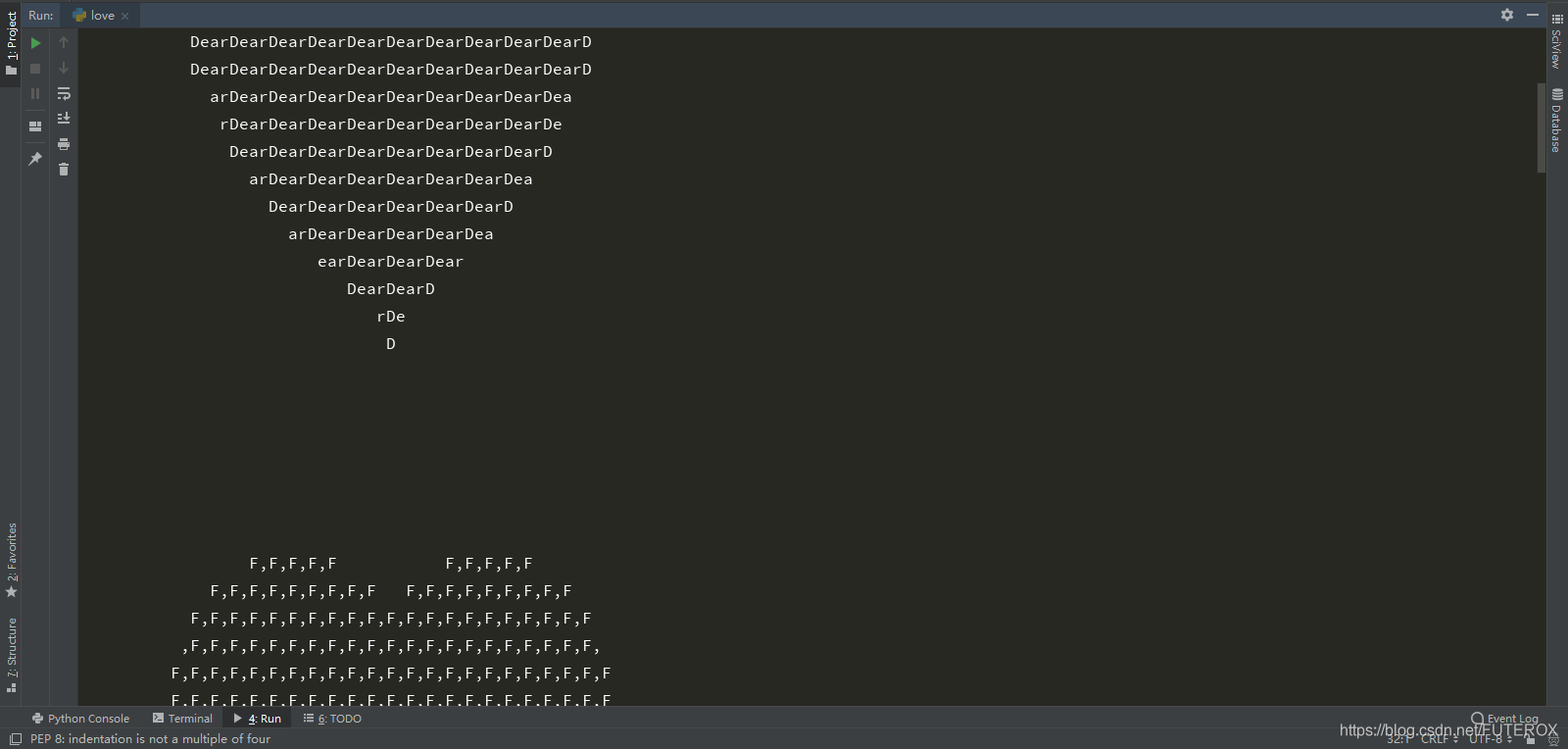代码如下 import timesentence = "Dear F, I love you forever!"for char in sentence.split(): allChar = [] for y in range(15,-15,-1): lst = [] lst_con = '' for x in range(-30, 30): formula = ((x*0.05)**2+(y*0.1)**2-1)**3-(x*0.05)**2*(y*0.1)**3 if formula <= 0: lst_con += char[(x) % len(char)] else: lst_con += ' ' lst.append(lst_con) allChar += lst print('\n'.join(allChar)) time.sleep(2)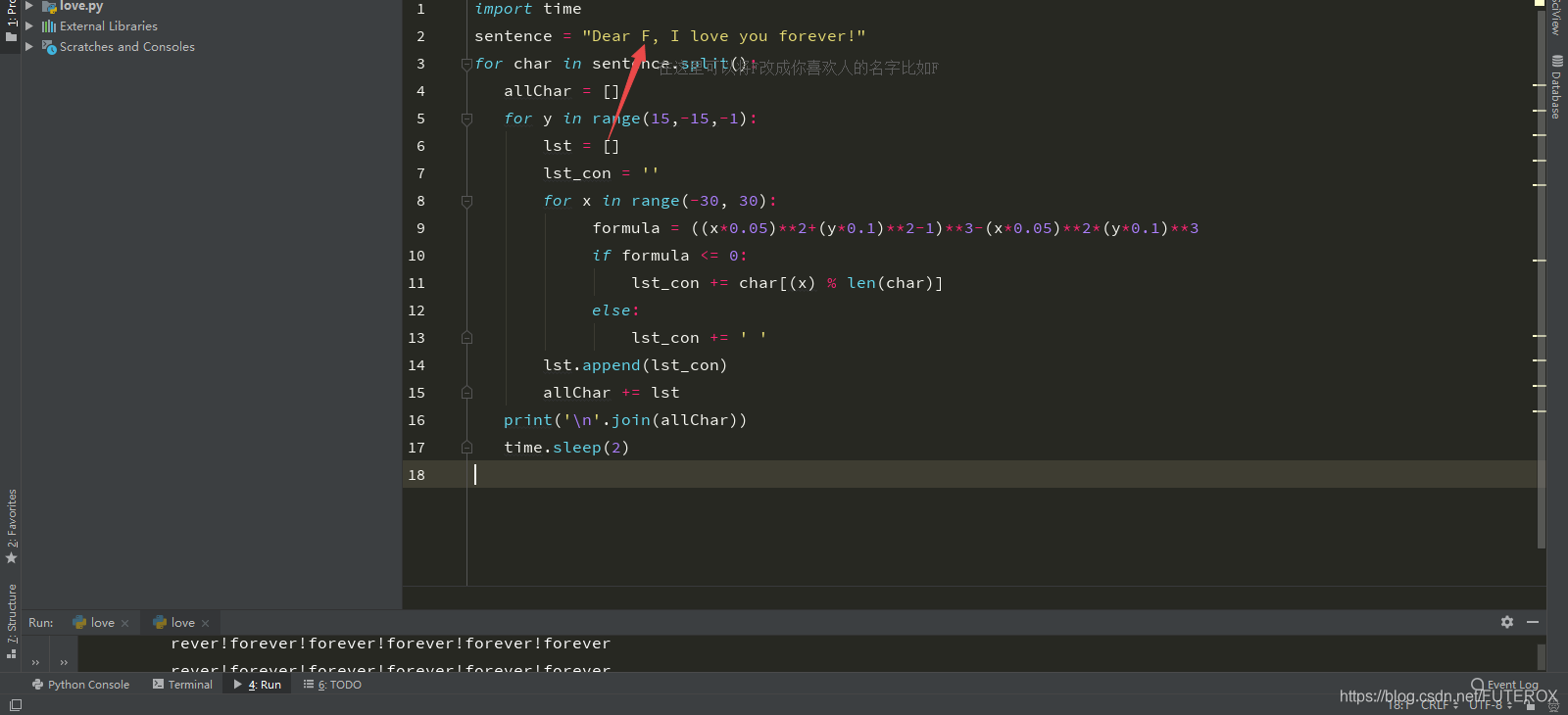 
使用图形turtle（后期在爬虫系列会讲到！！！）
这个卖个关子以后详细将这个库。（画个玫瑰，经典的入门项目）
先说一下有哪些用法 turtle.fillcolor(colorstring) 绘制图形的填充颜色 turtle.color(color1, color2) 同时设置pencolor=color1, fillcolor=color2 turtle.filling() 返回当前是否在填充状态 turtle.begin_fill() 准备开始填充图形 turtle.end_fill() 填充完成 turtle.hideturtle() 隐藏画笔的turtle形状 turtle.showturtle() 显示画笔的turtle形状 turtle.forward(distance) 向当前画笔方向移动distance像素长度 turtle.backward(distance) 向当前画笔相反方向移动distance像素长度 turtle.right(degree) 顺时针移动degree° turtle.left(degree) 逆时针移动degree° turtle.pendown() 移动时绘制图形，缺省时也为绘制 turtle.goto(x,y) 将画笔移动到坐标为x,y的位置 turtle.penup() 提起笔移动，不绘制图形，用于另起一个地方绘制 turtle.circle() 画圆，半径为正(负)，表示圆心在画笔的左边(右边)画圆 setx( ) 将当前x轴移动到指定位置 sety( ) 将当前y轴移动到指定位置 setheading(angle) 设置当前朝向为angle角度 home() 设置当前画笔位置为原点，朝向东。 dot® 绘制一个指定直径和颜色的圆点 turtle.clear() 清空turtle窗口，但是turtle的位置和状态不会改变 turtle.reset() 清空窗口，重置turtle状态为起始状态 turtle.undo() 撤销上一个turtle动作 turtle.isvisible() 返回当前turtle是否可见 stamp() 复制当前图形 turtle.write(s [,font=(“font-name”,font_size,“font_type”)]) 写文本，s为文本内容，font是字体的参数，分别为字体名称，大小和类型；font为可选项，font参数也是可选项 这里的话我只用了： turtle.forward(distance) turtle.right(degree) turtle.left(degree) turtle.goto(x,y) turtle.hideturtle() turtle.fillcolor(colorstring) turtle.begin_fill() turtle.end_fill() turtle.write(s [,font=(“font-name”,font_size,“font_type”)]) setheading(angle) turtle.circle() 效果如下：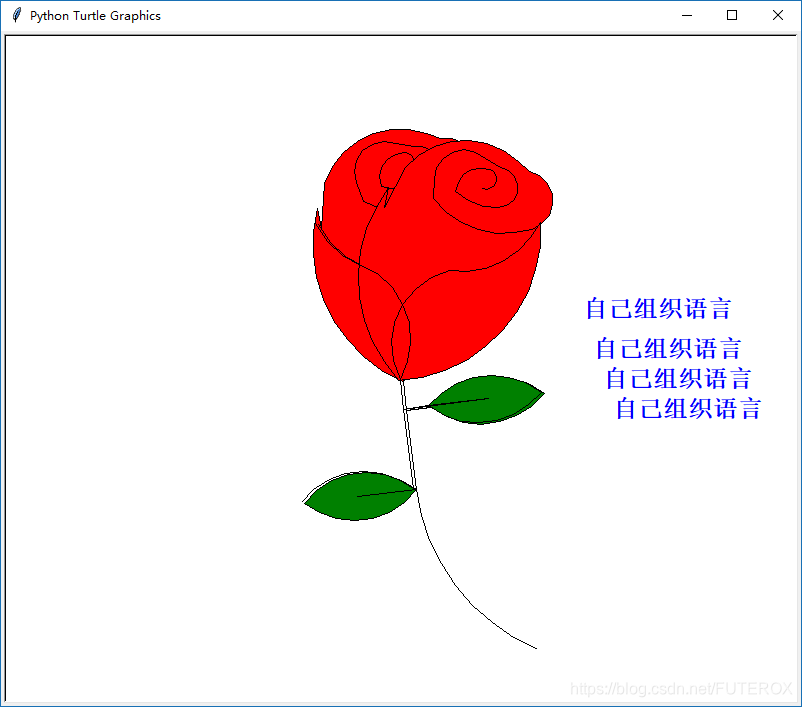
由于时间关系代码是赶出来的有些乱，不过还是可以用用的！！ import turtleimport timeturtle.hideturtle()turtle.penup()turtle.goto(180, 50)turtle.color("blue")time.sleep(1)turtle.write("自己组织语言", font=("Times", 18, "bold"))turtle.goto(190, 10)time.sleep(1)turtle.write("自己组织语言", font=("Times", 18, "bold"))turtle.goto(200, -20)time.sleep(1)turtle.write("自己组织语言", font=("Times", 18, "bold"))turtle.goto(210, -50)time.sleep(1)turtle.write("自己组织语言", font=("Times", 18, "bold"))#turtle.goto(200,-80)不够再加#turtle.write('自己组织语言',font=("Times", 18, "bold"))不够再加！！！turtle.goto(0, 0)turtle.color("black")turtle.penup()turtle.left(90)turtle.fd(200)turtle.pendown()turtle.right(90)turtle.fillcolor("red")turtle.begin_fill()turtle.circle(10, 180)turtle.circle(25, 110)turtle.left(50)turtle.circle(60, 45)turtle.circle(20, 170)turtle.right(24)turtle.fd(30)turtle.left(10)turtle.circle(30, 110)turtle.fd(20)turtle.left(40)turtle.circle(90, 70)turtle.circle(30, 150)turtle.right(30)turtle.fd(15)turtle.circle(80, 90)turtle.left(15)turtle.fd(45)turtle.right(165)turtle.fd(20)turtle.left(155)turtle.circle(150, 80)turtle.left(50)turtle.circle(150, 90)turtle.end_fill()turtle.left(150)turtle.circle(-90, 70)turtle.left(20)turtle.circle(75, 105)turtle.setheading(60)turtle.circle(80, 98)turtle.circle(-90, 40)turtle.left(180)turtle.circle(90, 40)turtle.circle(-80, 98)turtle.setheading(-83)turtle.fd(30)turtle.left(90)turtle.fd(25)turtle.left(45)turtle.fillcolor("green")turtle.begin_fill()turtle.circle(-80, 90)turtle.right(90)turtle.circle(-80, 90)turtle.end_fill()turtle.right(135)turtle.fd(60)turtle.left(180)turtle.fd(85)turtle.left(90)turtle.fd(80)turtle.right(90)turtle.right(45)turtle.fillcolor("green")turtle.begin_fill()turtle.circle(80, 90)turtle.left(90)turtle.circle(80, 90)turtle.end_fill()turtle.left(135)turtle.fd(60)turtle.left(180)turtle.fd(60)turtle.right(90)turtle.circle(200, 60)turtle.penup()turtle.color("blue")turtle.hideturtle()turtle.penup()turtle.goto(0, 0)turtle.color("black")turtle.penup()turtle.left(90)turtle.fd(200)turtle.pendown()turtle.right(90)turtle.fillcolor("red")turtle.begin_fill()turtle.circle(10, 180)turtle.circle(25, 110)turtle.left(50)turtle.circle(60, 45)turtle.circle(20, 170)turtle.right(24)turtle.fd(30)turtle.left(10)turtle.circle(30, 110)turtle.fd(20)turtle.left(40)turtle.circle(90, 70)turtle.circle(30, 150)turtle.right(30)turtle.fd(15)turtle.circle(80, 90)turtle.left(15)turtle.fd(45)turtle.right(165)turtle.fd(20)turtle.left(155)turtle.circle(150, 80)turtle.left(50)turtle.circle(150, 90)turtle.end_fill()turtle.left(150)turtle.circle(-90, 70)turtle.left(20)turtle.circle(75, 105)turtle.setheading(60)turtle.circle(80, 98)turtle.circle(-90, 40)turtle.left(180)turtle.circle(90, 40)turtle.circle(-80, 98)turtle.setheading(-83)turtle.fd(30)turtle.left(90)turtle.fd(25)turtle.left(45)turtle.fillcolor("green")turtle.begin_fill()turtle.circle(-80, 90)turtle.right(90)turtle.circle(-80, 90)turtle.end_fill()turtle.right(135)turtle.fd(60)turtle.left(180)turtle.fd(85)turtle.left(90)turtle.fd(80)turtle.right(90)turtle.right(45)turtle.fillcolor("green")turtle.begin_fill()turtle.circle(80, 90)turtle.left(90)turtle.circle(80, 90)turtle.end_fill()turtle.left(135)turtle.fd(60)turtle.left(180)turtle.fd(60)turtle.right(90)turtle.circle(200, 60)turtle.penup()turtle.color("blue")turtle.goto(0, 200)turtle.fillcolor("red")turtle.begin_fill()turtle.circle(10, 180)turtle.circle(25, 110)turtle.left(50)turtle.circle(60, 45)turtle.circle(20, 170)turtle.right(24)turtle.fd(30)turtle.left(10)turtle.circle(30, 110)turtle.fd(20)turtle.left(40)turtle.circle(90, 70)turtle.circle(30, 150)turtle.right(30)turtle.fd(15)turtle.circle(80, 90)turtle.left(15)turtle.fd(45)turtle.right(165)turtle.fd(20)turtle.left(155)turtle.circle(150, 80)turtle.left(50)turtle.circle(150, 90)turtle.end_fill() 200多行，为了你的那个TA真不算多！！！
最后一个方法
现在离开你的电脑面前，去楼下花店，在5.20那一天，买9多玫瑰写下一封你的表白信。你可以选择留下花儿和信，但请你记住不要再留下一封匿名信。也许你还犹豫不定，但我想当你看到这最后一个方法的时候，心中已经有了答案！
转载地址：http://gxfxz.baihongyu.com/
你可能感兴趣的文章